There’s more than one way to work with numbers in Java. We have access to 7 numeric primitive types and their boxed counterparts, high-precision object types, multiple concurrency-akin types and helpers, and more.

This article will take a look at some of these different types, their pros and cons, and how and when to use them.

Understanding Primitive Data Types

Primitive types, as their name suggests, are the most basic data types available to us. They represent raw values and are treated differently from objects.

Here’s the list of Java’s seven numeric primitive types, including their bit-size and range:

The ranges for float and double are a little bit complicated, as floating-point numbers have min and max ranges for both negative and positive values. If you’re interested to learn more, you can check out the Java Language Specification (§ 2.3.2) or the underlying IEEE Standard 754 for Floating-Point Arithmetic.

The characteristics of primitive type stem from being raw values, and they are best compared based on that assumption.

No Methods Available

Primitive types don’t have any methods or constructors. They’re created using literals instead:

int i = 42;

long l = 23L;

float f = 3.14F;

Memory Footprint

Without any additional methods or attributes, like metadata or an object header, primitives have a small and fixed size.

It’s true that primitive types have a fixed size, but it depends on the actual JVM implementation. For example, boolean represents a 1-bit value. However, the JVM has limited support for it, and maps it to an int, and boolean[] to short[] (see JVM Spec 2.3.4). This is an implementation detail and depends on the JVM you’re using.

The object-based counterparts to primitives require 128 bits, and Long and Double even require 192 bits for a single instance!

For primitive arrays, calculating the size is a little bit more complicated. Java arrays are objects, regardless of whether they hold primitive types or not. That requires 12 bytes for the object header plus another 4 bytes for the array’s size. Taking the reference to the array into account (another 8 bytes) creates the overhead to store the int values of 24 bytes.

To make it even more complicated, memory is rounded up to multiples of 8 bytes for memory alignment, even if less memory is theoretically needed. See the following graph for how different primitive arrays behave:

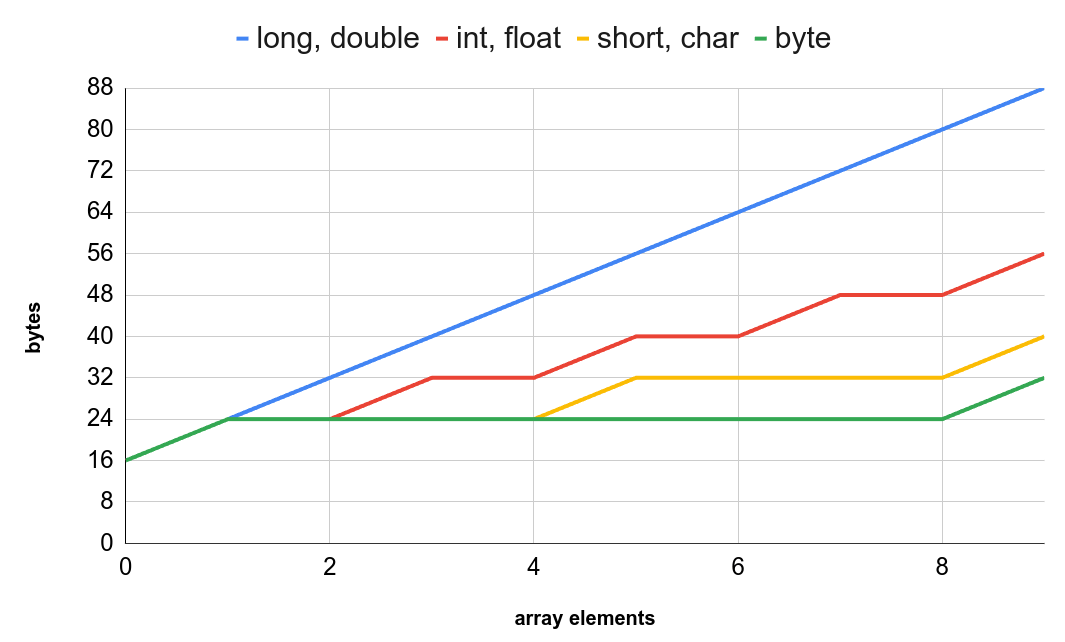
Keep in mind that the actual memory usage can vary slightly between different JVM implementations and settings.

Still, the actual size of simple int is fixed and always 4 bytes.

The fixed size makes it possible for primitive values to live on the Stack, unlike Objects, which reside on the Heap.

But what does that actually mean, and why does it matter? Ultimately, Heap and Stack are both located in the RAM anyway.

Storage Location

The main difference is the “closeness” of data to the thread executing the Java code. The Heap is, well a heap of objects, and all of the running Java code references objects from it. That’s why it needs a garbage collector, as anyone could hold a reference to any object.

On the other hand, the Stack is bound to the current Stack frame.

Each time a method is invoked, a new stack frame is created with its own Stack memory to hold local primitive values and references to objects on the Heap. This memory is discarded when the methods end, as it’s no longer needed.

The magic word here is “local”. A primitive field in an object used in a method still lives on the Heap, as it’s not part of the current stack frame, at least not directly. The reference to object is on the Stack, the primitive field of the object on the Heap. At least in theory, because it’s an JVM implementation detail how memory is treated. Compiler optimizations like escape analysis might move an object completely to the Heap, if it’s allocated locally and never _escapes".

Having memory bound to the current method allows for generally faster access and manipulation. The allocations are typically contiguous, creating spatial locality, making it easier for the processor to cache that memory, reducing memory access times.

Identity

Another advantage of raw values is their identity behavior. As they ARE the value and not just a memory address, the value IS the identity, allowing us to use ==, etc., for comparisons. Well, we NEED to use them, as there are no methods available in the first place.

For the floating-point types, though, we should use the static compare helpers on the wrapper types, as they mitigate the issues of comparing floating-point types for equality:

java.lang.Float:  boolean compare(float, float)
java.lang.Double: boolean compare(double, double)

The other primitive wrappers also have compare methods, but they just use the most sensible operator-based code, like for int:

// java.lang.Integer
public static int compare(int x, int y) {
    return (x < y) ? -1 : ((x == y) ? 0 : 1);
}

Default Values

Primitives don’t support null but use a zero-equivalent instead. Although it’s nice not to have to worry about triggering a NullPointerException, the lack of nullability introduces the issue of how to represent the absence of a value.

Without null, “no value” is represented by a valid value, making it impossible to discern the two states. Usually, we have to do it ourselves, like not using zero as a valid value or using -1 if our required range is only positive.

If we need to discern the different states, we can either use the primitive’s wrapper type, or one of the specialized Optional... types.

No Generics

In short, we can’t use primitive types as generic types. For some use cases, like Optionals, Streams, and functional interfaces, there are specialized types already available in the JDK. However, not all scenarios are covered, and we might need to switch to wrapper types.

Still, there’s light on the horizon in the form of Project Valhalla, which aims to bridge the gap between primitive and object types. The project’s primary goal is to introduce value types, combining the abstractions of OO programming with the performance characteristics of simple primitives.

It’s an ongoing project, with certain JEPs available in early-access builds. I imagine that it will take a lot of time and more Java versions until it will become generally available, as it’s an impactful change and will significantly shape the future of the Java language and the JVM.

Conclusion (Primitives)

Primitives are fast and require less memory compared to their object-based counterparts. So, if possible, we should stick to primitive types over the alternatives.

However, there are also downsides attached to primitive types:

• No concept of “no value”
• Not usable for parameterized types
• Requires specialized types for specific use cases

Wrapper Types and Auto-Boxing

Where primitive types are “the most primitive” representation of a value, wrapper types “wrap” the actual value into an object as a reference type.

Each primitive type has a counterpart located in the java.lang package:

All wrapper types, except for Character, inherit from the Number class, simplifying the conversion to their primitive counterparts.

Being full-fledged objects also means all the associated overhead: they are allocated on the Heap while their references are stored on the Stack.

This results in increased memory usage and reduced performance in comparison to primitive types. But there are benefits to being an object as well.

Parameterized Types

The wrapper types are full-fledged objects that can be used as parameterized types, with all their pros and cons.

For example, using a List<Integer> provides much additional functionality compared to an int[]. However, it performs worse and requires more memory to do its job. Still, in most real-world scenarios, where we don’t need every single CPU cycle and every bit of memory, the advantages the Collection types provide outweigh their downsides.

Like always, don’t optimize too early. If in doubt, measure first!

Providing Functionality (for Primitives)

Looking at the documentation of Integer, for example, we discover a plethora of methods and other goodies available to use.

At closer inspection, however, a lot of the methods are static and accept primitive values. In a way, the wrapper types are used to aggregate methods for the primitive types, as they can’t have any.

Autoboxing

Autoboxing is the automatic conversion between primitive types and their object-based wrapper counterparts so they can be used indiscriminately:

// PRIMITIVE
int smallInt = 42;

// AUTOBOX TO WRAPPER
Integer bigInt = smallInt;

// ARITHMETIC OPERATION USES (UN)BOXING, TOO
bigInt += 23;

System.out.println(bigInt + " -> " + bigInt.getClass());
// 65 -> class java.lang.Integer

This automagical interoperability is great, as we don’t have to think much about it, but it also introduces a few problems that we need to keep in mind.

The actual boxing and unboxing conversions are listed in the JLS § 5.1.7 and § 5.1.8

First, autoboxing isn’t free and can have a significant performance impact if used in loops, etc. That’s why many common operations have specialized types so we can rely on a more object-type-like developer experience but still use primitives under the hood.

Second, the problem with null…

Nullability of Wrapper Types

Any object reference can be null, including the primitive wrapper types. On the one hand, it’s great to have a state representing “not initialized/no value at all”. But it comes with all the problems of the billion-dollar mistake. And thanks to autoboxing, it also affects arithmetic operations when mixing primitives and wrappers.

One solution is to use one of the Optional types with either the wrapper or directly the primitive type. Sure, another “box” to put the value into creates even more overhead… But if a NullPointerException occurs, no one ever says, “well, at least it had the smallest overhead possible up to this point”.

Using Optional<T> is straightforward, as it’s the same for all reference types. I’ll discuss the specialized primitive Optional...types shortly.

Identity Crisis

Java has different methods of comparing objects and primitives, each with its own semantics. Using the “wrong” one, like using == for non-primitives, leads to unexpected results and introduces subtle, hard-to-catch bugs.

However, let’s check out the following code:

Integer lhs = 42;
Integer rhs = 42;

System.out.println(lhs == rhs);
// true

Let’s check again with another value…

Integer lhs = 128;
Integer rhs = 128;

System.out.println(lhs == rhs);
// false

What the hell is going on here?

Let’s make it even worse…

int lhs = 128;
Integer rhs = 128;

System.out.println(lhs == rhs);
// true

Actually, everything works as intended. But this not-so-obvious behavior caught me by surprise in the past.

Using == compares the value of a variable. For primitives, that’s the actual raw value, and for the wrapper types, it’s the object’s memory address.

The first comparison of an Integer with the 42 succeeds using == because lhs and rhs are actually the same object. Autoboxing internally uses the static valueOf method on Integer to box up the int literal. If we look at the documentation, it states that the method always caches values from -128 up to 127, and maybe even more. The comparison fails because the second example is just outside the cached range.

The third one mixes primitives and non-primitives, so autoboxing is used. The actual comparison eventually occurs between two int values, so it succeeds.

As you can see, a comparison can “fail successfully” if == is used. That’s why we should always use the wrapper type’s static boolean compare(int, int) instead:

Integer lhs = 128;
Integer rhs = 128;

System.out.println(Integer.compare(lhs, rhs) == 0);
// true

Be aware that the Long type uses the same caching behavior for the range -128 to 127.

Conclusion (Wrapper Types)

Wrapper types often feel like a band-aid to bridge the gap between Java’s OO-centric design and primitive value types. However, they are needed until Project Valhalla takes off, so we need to live with their downsides compared to using simple primitives.

In many real-world scenarios, though, the performance impact is marginal in the overall picture or can be minimized if we reduce autoboxing as much as possible.

As with all language features and special types, we need to know about their edge cases, like nullability, to utilize them safely.

High-Precision Math

Most simple calculations can be done with primitive types like int or long for whole numbers and float or double for floating-point calculations. However, there are multiple issues with the primitives: a limited range and precision.

BigInteger

Both int and Integer share the same range of -2'147'483'648 to 2'147'483'647 (-2³¹ to 2³¹-1).

A little over 2 billion is a lot, but maybe it’s not enough for your use case.

That’s where java.math.BigInteger comes into play.

It’s a specialized type representing immutable arbitrary-precision integers (the math kind, not the programming language kind). The type doesn’t support autoboxing, as its range is “a little bit” wider:

-2^{Integer.MAX_VALUE} to 2^{Integer.MAX_VALUE} (both exclusively).

And that’s just the guaranteed range! Depending on your JVM, it might be even more.

For arithmetic operations, the type mimics the available arithmetic operators with methods like add(BigInteger) for +, and multiply(BigInteger) for *, and so forth.

One thing we MUST be aware of is the type’s immutability. Calling add won’t add the value to the current instance but will return a new instance with the result instead:

BigInteger bigInt1 = new BigInteger("42");
BigInteger bigInt2 = new BigInteger("23");

BigInteger sum = bigInt1.add(bigInt2);

System.out.println("Sum: " + sum.toString());
// => 65

System.out.println("Unchanged bigInt1: " + bigInt1.toString());
// => 42

To not forget to use the result, I try to follow these “rules” in my code:

• Use calculation directly as an expression.
• Combine multiple calculation steps into a fluent call.
• If it is too complicated for a fluent call, split it up, but don’t re-assign the original variable. Each step needs to use its own variable.

Still not a perfect system, but it mitigates the overall problem at least a little.

BigDecimal

Where BigInteger increases the usable range manifold, the BigDecimal type is primarily about precision.

Dealing with floating points is always a nightmare. Take the following example:

double val = 0.0D;
for (var idx = 1; idx <= 11; idx++) {
    val += 0.1D;
}

System.out.println(val);

What do you think is the result of adding 0.1D ten times to zero?

The mathematically correct answer is 1.1.

However, the println will show Java sums it up to 1.0999999999999999.

That’s why we need a type like BigDecimal that solves the floating-point problem by using an unscaled arbitrary precision integer in combination with a 32-bit scale.

A zero or a positive scale indicates the number of digits to the right of the decimal point. A negative scale means that the number’s unscaled value is multiplied by ten raised to the absolute value of the scale.

Therefore, the BigDecimal value is:

unscaledValue * 10^-scale

Like its integer-based brethren, it mimics arithmetic operations by giving us a huge set of methods. This time, however, we need to specify either a RoundingMode or use a MathContext to get the expected precision and results.

Thanks to its precision, the previous example of adding up 0.1 now has the correct result:

var val = BigDecimal.ZERO;
var step = new BigDecimal("0.1");

for (var idx = 1; idx <= 11; idx++) {
    val = val.add(step);
}

System.out.println(val);
// 1.1

So you see, BigDecimal is perfect when precise numerical computation is crucial.

Specialized Types for Primitives

The wrapper types as an alternative for scenarios like parameterized types or Collections are nice “nice-to-have” additions and are often good enough. Still, the performance and memory implications sometimes require a primitive-based solution.

Thankfully, the JDK has covered some of the common use cases.

The Absence of a Value

Depending on our use case, the zero-equivalent default values of primitives can be problematic. With a real null, it’s hard to represent the absence of a value without using a magic number.

Being able to represent nothingness, compared to not-initialized/default value, can be an advantage. That’s why Java introduced primitive variants of Java 8’s Optional<T> type:

• java.util.OptionalInt
• java.util.OptionalLong
• java.util.OptionalDouble

Not all primitive types are available, but it’s a start, and so far, I haven’t missed the others.

Compared to Optional<T>, the types are quite, well, primitive (pun intended). They lack methods like filter, map, or flatMap. But their primary goal, representing an optional value, is still there.

Functional Interfaces

I’m a huge fan of Java’s functional Renaissance that began with Java 8. However, the “primitive vs. wrapper types” problem spoils the party, at least to some degree. That’s why Java included specialized functional interfaces for many use cases.

To not mention each primitive type all the time, the following part of the article will mostly mention int. But it also applies to long and double. Other primitive types didn’t get special treatment, just like the Optional... types.

The primary four functional interfaces are:

• T Supplier<T>#get()
  Takes no arguments, but returns an object. A method reference to a simple POJO-Getter qualifies as a Supplier.
• void Consumer<T>#accept(T)
  Takes a single argument and doesn’t return anything. Every POJO-Setter qualifies as a Consumer.
• R Function<T, R>#apply(T)
  Takes a single argument and returns an object.
• boolean Predicate<T>#test(T)
  A specialized function that accepts an object and returns a boolean primitive.

Each of them has a specialized variant:

• int IntSupplier#getAsInt()
• void IntSupplier#accept(int)
• R IntFunction#apply(int)
• boolean IntPredicate#test(int)

There are a lot more specialized functional interfaces available, like IntUnarayOperator, which accepts and returns an int. Or functional interfaces for conversion between primitive types, etc.

Check out one of my previous articles for a more comprehensive list of the available interfaces.

Primitive Streams

There are specialized ...Stream variants available, so we don’t need to rely on autoboxing:

• IntStream
• LongStream
• DoubleStream

They have static factory methods available, like of(...), range(...), or iterate(...).

The following methodsa are available for int, long, and double respectively.

But we can also map a Stream<T> to a primitive one:

• IntStream mapToInt(ToIntFunction<T> mapper)
• IntStream mapMultiToInt(BiConsumer<? super T,? super IntConsumer> mapper)
• IntStream flatMapToInt(Function<T, IntStream> mapper)

This way, we don’t need to use autoboxing even when we start out with objects:

long[] hashCodes = Stream.of("hello", "world")
                         .mapToInt(String::hashCode)
                         .toArray();

Primitive Collections

The Collection API has a blindspot regarding primitive handling.

Even though ArrayList uses an array internally, there’s no support for primitive types. However, there’s Eclipse Collections which provides a plethora of specialized collection types, not just primitive ones.

If you need to deal with Lists and Maps holding primitives a lot, it definitely worth checking out the project.

Atomic Numbers

Java’s concurrency game gets better with every release. Still, working in a multi-threaded environment can make things quite difficult.

Working with int and long can be easily made thread-safe without using the synchronized keyword, by using their Atomic... types in the java.util.concurrent.atomic package:

• AtomicInteger
• AtomicIntegerArray
• AtomicLong
• AtomicLongArray

Atomic operations use a technique called compare & swap (CAS) to ensure data integrity.

A typical CAS operation works on three operands:

• The memory location of the variable
• The existing expected value
• The new value

The CAS operation checks if the existing value still matches the expected value and then updates it; otherwise, no update is happening. And the best thing is that it’s done in a single machine-level operation! That means no locks are required, and no threads are suspended.

While an Atomic... variable offers significant benefits, as usual, there are also several downsides to consider.

First, the performance might suffer in high contention. If multiple threads want to update the value, the CAS might waste a CPU cycles on retries, as the value might be changed by other threads. This becomes clearer when we look at the actual code. For example, the getAndSet method delegates to Unsafe#getAndSetInt:

@IntrinsicCandidate
public final int getAndSetInt(Object o, long offset, int newValue) {
  int v;
  do {
    v = getIntVolatile(o, offset);
  } while (!weakCompareAndSetInt(o, offset, v, newValue));
  return v;
}

The loop ensures the value is set eventually, but it might take a few loop runs under high contention.

Second, as with all non-primitive types, there’s the usual memory overhead compared to a simple primitive. However, that’s to be expected. You didn’t think we’d get atomic updates for free, did you?

Third, the atomic operation is restricted to the single variable it covers. Updating multiple (atomic or not) variables isn’t possible.

There are more potential pitfalls, mostly related to how concurrent code is always a complex beast to tackle, so I won’t go into more details, as it’s out of the scope of this article.

Conclusion

Working with numbers is an essential part of any program, but how to use them can range from simple primitives to more complex wrapper types, specialized functional interfaces, or arbitrary precision math types.

So what should I use when?

Well, it all depends on your requirements, but my general approach is:

• Use primitive types whenever possible
  Not only for performance-critical code, but all code in general. Not having to deal with nullability is a great plus, with the option to use a specialized Optional... type if a zero-equivalent default value isn’t enough.

• Be Mindful of Autoboxing
  Most of the time, at least for my use cases, it doesn’t matter too much. Still, be on the lookout for pitfalls like too much (un)boxing in loops, etc., as the performance penalties can add up quickly.

• Boxed Types Before Specializations
  The specialized types fill a certain need but can introduce an interoperability problem. A Consumer<Long> is still a Consumer<T>, whereas an IntConsumer is not. Usually, it’s easy to bridge between the types. However, it’s still more code. Plus, the specialized variants typically only support int, long, and double.

• Use BigDecimal for “real” math and money
  Primitives are fine for most arithmetic operations. But there are areas where you need every precision available to us, like dealing with monetary values or complex mathematical formulas. If the “correct” result is more important than performance or memory footprint, use BigDecimal.

• Only use BigInteger if you need the range or its methods
  The int primitive goes a long way, unless you need a wider range or one of its operations like GCD or primality testing.

However, most of these considerations become moot if you’re not dealing with critical high-performance code.

The most performant code won’t save you if it becomes unmaintainable in the process. Prioritizing the overall developer experience and code simplicity is paramount, except when it leads to genuine performance issues. I don’t say to neglect or even ignore performance completely, but to actually verify any problems before they warrant creating more complex code to save a few CPU cycles.

That being said, it’s not an invitation to disregard performance. Instead, focus on straightforward, easy-to-maintain code that favors primitives, but don’t try to force it just because you can.

Interested in using functional concepts and techniques in your Java code?

Check out my book!

Available in English, Polish, and soon, Chinese.

Resources

• Primitive Data Types (Java Documentation)
• Project Valhalla (OpenJDK)
• Java Primitives Versus Objects (Baeldung)
• Memory Layout of Objects in Java (Baeldung)